Uma forma de avaliar se geradores de números aleatórios (GNA) são confiáveis é testando a convergência deles. Podemos escolher um estimador qualquer, a média amostral por exemplo, e avaliar se este estimador converge para o seu valor esperado (teórico). Vamos testar aqui se utilizar um gerador de números inteiros é mais eficiente do que um gerador de números reais truncados, ou seja, vamos testar se o truncamento de números reais introduz algum viés na geração da série de números aleatórios.

Para um GNA que gera apenas inteiros 0 e 1 com chances iguais, temos como valor esperado para a média 0.5. O GNA de números reais do Python (módulo random) gera números no intervalo [0.0, 1.0) de maneira uniforme. Se o gerador for realmente uniforme, então podemos multiplicar o seu resultado por 2 e tomar o seu floor, pegando assim o número inteiro maior ou igual ao número fornecido. Como estamos fazendo [0.0, 1.0)*2, temos portanto números reais no intervalo [0.0, 2.0). Tomando o floor de qualquer número nesse intervalo temos apenas 0 e 1. Como estamos considerando que o gerador é uniforme e bastante homogêneo, então o valor esperado para a média de uma sequência produzida dessa forma é também 0.5.

Os programas abaixo geram N=1000 números aleatórios e calculam a média amostral para cada iteração. A série da evolução da média amostral é colocada em um gráfico.

Usando random truncado

   1 from pylab import *
   2 from numpy import zeros, array
   3 import random
   4 import math
   5 
   6 N = 1000
   7 z = zeros(N)
   8 i = 0
   9 s = 0
  10 while i < N:
  11     x = math.floor(random.random()*2)
  12     s += x
  13     z[i] = float(s)/(i+1)
  14     i += 1
  15 
  16 figure(1)
  17 plot(z)
  18 axhline(y=0.5)
  19 ylim(0.0,1.0)
  20 yticks([0.0, 0.5, 1.0])
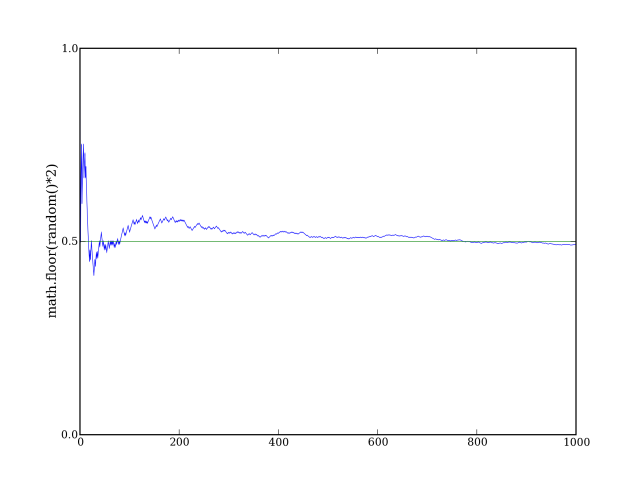
  21 ylabel('math.floor(random()*2)')

Este programa gerou o seguinte gráfico.

Usando randint(0,1)

   1 from pylab import *
   2 from numpy import zeros, array
   3 import random
   4 import math
   5 
   6 N = 1000
   7 z = zeros(N)
   8 i = 0
   9 s = 0
  10 while i < N:
  11     x = random.randint(0,1)
  12     s += x
  13     z[i] = float(s)/(i+1)
  14     i += 1
  15 
  16 figure(2)
  17 plot(z)
  18 axhline(y=0.5)
  19 ylim(0.0,1.0)
  20 yticks([0.0, 0.5, 1.0])
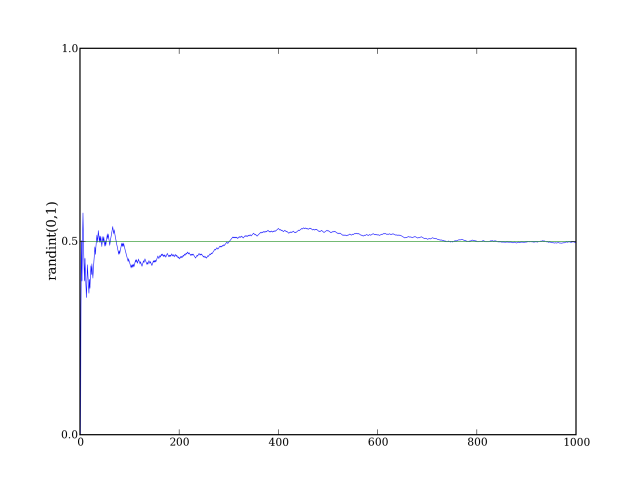
  21 ylabel('randint(0,1)')
  22 show()

Este programa gerou o seguinte gráfico.

Conclusão

Podemos observar que a convergência para a média amostral em ambos os programas é bastante semelhante e pelo menos neste teste grosseiro não é possível identificar que o truncamento introduz algum viés na amostra.